阴阳师中的御怨般若在经过这次的修改之后一下成为了斗技中的大热门角色,整个式神的战斗力一下次提升了几个档次,但是不少使用芋圆的玩家们可能会发现,在高速御魂的加成下,经常会发生第二次行动无法超车的情况,白白错失了一次行动的机会,损失非常大,那么应该如何配速才能保证芋圆能够正常超车呢?下面就给大家带来阴阳师高速御怨般若配速方法。
1)当阵容中没有拉条时
当芋圆速度=1.65*待超车式神速度时,大招自拉条后,与待超车式神同时到达行动条。(并因为同时到达时高速者先动而先出手)
套用公式:x=1.65*待超车式神速度
1=行动条总长度
x=芋圆速度
y=低速速度
1/x=芋圆第一轮经过时间
y*1/x=低速式神已跑距离
低速剩余时间:1/y-1/x
芋圆需跑距离:1*0.65
芋圆与低速同时到达:(1/y-1/x)*x=1*0.65
x/y-1=0.65
x=1.65*y
结论1-1:当阵容中无拉条时,御怨般若第二次行动若要超车己方低速,则御怨般若速度需大于等于低速速度的1.65倍。
2)当阵容中有拉条时
1=行动条总长度
x=芋圆速度
y=低速速度
z=拉条速度
2-1)若x
由于一速拉条理论最快284(面灵气理论极限御魂),且本情形低速被拉条,芋圆超车难度大于上一情形,因此芋圆速度必定大于上一情形的1.65*y
取y=130,1.65*y=214.5,由于一速拉条拉起二速不被超车阈值为284*0.7=198.8,由214.5>198.8,即此情形下芋圆必然无法享受一速拉条的完整拉条效果(只被拉了低于30%的行动条就已到达行动条顶端)
根据上述分析,芋圆享受拉条效果低于30%,故拉条完毕后芋圆已立即到达行动条顶部而无需自身再跑,故第一轮芋圆跑过时间=一速拉条跑过时间。
第一轮拉条跑过时间 = 1/z
第一轮芋圆跑过时间 = 1/z
第一轮低速跑过时间 = 1/z
第一轮低速跑过距离 = 1/z*y+0.3
第一轮低速剩余时间 = [1-(1/z*y+0.3)]/y = 0.7/y-1/z
芋圆大招满面具自拉条后需跑距离 = 1-0.35 = 0.65
芋圆和低速同时到达行动条顶端:(0.7/y-1/z)*x=0.65
x=0.65/(0.7/y-1/z)
公式可见z越大,x越小。
代入y=130,z=284,则x=348.81,该速度远远超出理论极限,且不符合大前提x
故芋圆慢于拉条时,芋圆永远不可能成功套圈己方低速。
结论2-1:当阵容中有拉条时,若御怨般若慢于拉条,则御怨般若第二次行动若要超车己方低速所需条件超出理论极限,即此情形下御怨般若永远不可能成功套圈己方低速。
2-2)若x>z,即芋圆快于拉条,一速芋圆,二速拉条。
由于芋圆快于拉条,拉条行动时芋圆已开完大招、已触发完毕满面具自拉条,且已于自身第二轮先行跑动一段距离。
第一轮芋圆跑过时间 = 1/x
第一轮拉条跑过时间 = 1/z
由于x>z,可知1/x<1/z,芋圆先到达行动条顶部。
拉条到达行动条顶部时,第二轮芋圆已跑距离 = (1/z-1/x)*x+0.35 = 1*x/z-0.65
拉条到达行动条顶部时,低速已跑距离 = 低速速度乘以拉条跑过时间 = 1/z*y
2-2-1)若第二轮芋圆已跑距离大于等于低速已跑距离:
若第二轮芋圆已跑距离大于等于低速已跑距离,由于芋圆速度大于低速,若条件成立,拉条相同幅度后必然芋圆先动,超车成功。
此时有:1*x/z-0.65≥1/z*y
化简:x-0.65*z≥y
x≥y+0.65*z
可见x线性正相关于z
结论2-2-1:当阵容中有拉条时,若御怨般若快于拉条,若拉条行动时第二轮御怨般若已跑距离大于等于低速已跑距离,则御怨般若第二次行动超车己方低速必然成功。此时御怨般若速度需大于等于低速速度加上0.65倍的拉条速度。
设低速130,代入实际情形具体观察:
代入y=130,则x≥130+0.65*z
设拉条速度z通常范围:130~277 ——出于御魂通常情况考虑,忽略拉条速度连130都不到的情形。
则x对应线性正相关范围:214.5~310.05
显然上限310不可能达到。
由芋圆基础速度115,御魂加成理论最大速度18*6+57=165,故芋圆理论最大速度280
代入公式,x=280时,z=230.77,故实际上限仅有230.77
即低速130时,拉条速度z不能高于230.77,否则芋圆所需速度x超出理论极限。
小结:结论2-2-1中,当低速y=130时,若拉条速度z∈[130,230.77],对应所需芋圆速度x∈[214.5,280]
引申结论2-2-1:当阵容中有拉条时,若御怨般若快于拉条,设己方低速130,若拉条行动时第二轮御怨般若已跑距离大于等于低速已跑距离,当拉条速度z∈[130,230.77]时,对应的超车低速所需御怨般若速度x∈[214.5,280]。
2-2-2)若第二轮芋圆已跑距离小于低速已跑距离:
反向使用公式2-2-1,若第二轮芋圆已跑距离小于低速已跑距离,必然有大前提"甲":x
2-2-2-1)若低速已跑距离大于等于0.7,拉条完毕后低速已达行动条顶,芋圆超车必然失败。因此情形2-2-2-1直接排除。
2-2-2-2)若低速已跑距离小于0.7,拉条完毕后低速尚未到达行动条顶,芋圆尚有超车可能(但不一定成功超车)。
设第二轮芋圆已跑距离小于低速已跑距离,芋圆若要超车必然有大前提"乙":1/z*y<0.7,化简:z>y*10/7
即第二轮芋圆已跑距离小于低速已跑距离,芋圆若要超车必然有大前提"乙":拉条速度需大于低速速度的10/7倍(1.4286倍)
综上所述:
大前提"甲":芋圆速度需小于低速速度加上0.65倍的拉条速度:x
大前提"乙":拉条速度需大于低速速度的10/7倍:z>y*10/7
由xx-0.65*z
由z>y*10/7得y<0.7*z
合并不等式得x-0.65*z<0.7*z
x<1.35*z
即芋圆速度需小于拉条速度的1.35倍
因芋圆快于拉条,故芋圆速度需介于拉条速度的1倍到1.35倍之间:z
前提2-2-2-2-a:当第二轮芋圆已跑距离小于低速已跑距离,芋圆若要超车必然有大前提:拉条速度需大于低速速度的10/7倍,且芋圆速度需介于拉条速度的1倍到1.35倍之间。
大前提有了,芋圆也就有了超车可能。
然而有了超车可能不代表一定超车成功,若要超车成功,则需:
若低速已跑距离小于0.7,拉条完毕后,第二轮芋圆已跑距离 = 1*x/z-0.65+0.3 = 1*x/z-0.35
若低速已跑距离小于0.7,拉条完毕后,第二轮芋圆剩余距离 = 1-[1*x/z-0.35] = 1.35-1*x/z
若低速已跑距离小于0.7,拉条完毕后,第二轮低速已跑距离 = 1/z*y+0.3
若低速已跑距离小于0.7,拉条完毕后,第二轮低速剩余距离 = 1-(1/z*y+0.3) = 0.7-1/z*y
设芋圆比低速更快,或者和低速同时到达行动条底,即芋圆跑过剩余距离所用时间小于等于低速所用时间:[1.35-1*x/z]/x≤(0.7-1/z*y)/y
化简:1.35/x-1/z≤0.7/y-1/z
1.35/x≤0.7/y
x≥y*27/14
前提2-2-2-2-b:当第二轮芋圆已跑距离小于低速已跑距离,芋圆若要超车,满足2-2-2-2-a的前提之下,芋圆速度需大于等于低速速度的27/14倍。
小结:
情形2-2-2-2若要超车成功,需满足以下全部条件:
(1)拉条速度需大于低速速度的10/7倍。
(2)芋圆速度需大于等于低速速度的27/14倍。
(3)芋圆速度需介于拉条速度的1倍到1.35倍之间。
设低速130,代入实际情形具体观察:
(1)拉条速度需大于185.71,即拉条速度∈[185.71,284]
(2)芋圆速度需大于等于250.71,即芋圆速度∈[250.71,280]
(3)芋圆速度需介于拉条速度的1倍到1.35倍之间
可见对于情形2-2-2-2,给定低速130时,拉条速度具有硬性下限185.71,芋圆速度具有硬性下限250.71。
满足以上两条硬性下限的前提下,只要符合芋圆速度介于拉条速度的1倍到1.35倍之间,即可超车成功。
取拉条速度为下限185.71,芋圆速度需介于185.71~250.71,可见芋圆速度恰好取拉条速度的1.35倍,在硬性下限250.71压线。
继续提高拉条速度,芋圆速度的选择范围随之提升而硬性下限固定不变。
结论2-2-2:当阵容中有拉条时,若御怨般若快于拉条,若拉条行动时第二轮御怨般若已跑距离小于低速已跑距离,则御怨般若第二次行动若要超车己方低速,需要满足三个条件:拉条速度需大于低速速度的10/7倍、御怨般若速度需大于等于低速速度的27/14倍、御怨般若速度需介于拉条速度的1倍到1.35倍之间。
引申结论2-2-2:当阵容中有拉条时,若御怨般若快于拉条,设己方低速130,若拉条行动时第二轮御怨般若已跑距离小于低速已跑距离,则御怨般若第二次行动若要超车己方低速,拉条速度需大于185.71,御怨般若速度需大于等于250.71,且御怨般若速度需介于拉条速度的1倍到1.35倍之间。
总结:
结论1-1:当阵容中无拉条时,则御怨般若第二次行动若要超车己方低速,则御怨般若速度需大于等于低速速度的1.65倍。
结论2-1:当阵容中有拉条时,若御怨般若慢于拉条,则御怨般若第二次行动超车己方低速所需的条件超出理论极限,即此情形下御怨般若永远不可能成功套圈己方低速。
结论2-2-1:当阵容中有拉条时,若御怨般若快于拉条,若拉条行动时第二轮御怨般若已跑距离大于等于低速已跑距离,则御怨般若第二次行动超车己方低速必然成功。此时御怨般若速度需大于等于低速速度加上0.65倍的拉条速度。
引申结论2-2-1:当阵容中有拉条时,若御怨般若快于拉条,设己方低速130,若拉条行动时第二轮御怨般若已跑距离大于等于低速已跑距离,当拉条速度z∈[130,230.77]时,对应的超车低速所需御怨般若速度x∈[214.5,280]。
结论2-2-2:当阵容中有拉条时,若御怨般若快于拉条,若拉条行动时第二轮御怨般若已跑距离小于低速已跑距离,则御怨般若第二次行动若要超车己方低速,需要满足三个条件:拉条速度需大于低速速度的10/7倍、御怨般若速度需大于等于低速速度的27/14倍、御怨般若速度需介于拉条速度的1倍到1.35倍之间。
备注1:若此时拉条速度小于低速速度的10/7倍,可能导致芋圆般若尚未来及追赶前,拉条就将低速式神拉到终点,此时超车失败。
备注2:若此时御怨般若速度大于拉条速度的1.5倍,将可能导致拉条行动时,芋圆般若已跑距离已经大于低速已跑距离。此时虽然可能导致超车成功,但是注意该情形已不再属于结论2-2-2范畴,而是属于结论2-2-1范畴,所需配速由结论2-2-1决定。
备注3:若此时拉条速度更进一步降低,而芋圆速度突破拉条速度的1.5倍更进一步提升,最终导致芋圆般若甚至能够套圈拉条式神本身,则拉条式神完全未能行动,形同虚设。此时虽然可能导致超车成功,但是注意该情形既不属于2-2-2范畴,也不属于结论2-2-1范畴,而是视为没有拉条的结论1-1范畴。
引申结论2-2-2:当阵容中有拉条时,若御怨般若快于拉条,设己方低速130,若拉条行动时第二轮御怨般若已跑距离小于低速已跑距离,则御怨般若第二次行动若要超车己方低速,拉条速度需大于185.71,御怨般若速度需大于等于250.71,且御怨般若速度需介于拉条速度的1倍到1.35倍之间。
备注:
结论2-2-1和结论2-2-2是两种"殊途同归"的算法,皆正确,分别在不同情形下实现御怨般若套圈己方低速。其中前者对拉条速度不要求下限,但具有上限,并随着拉条速度的增长而逐渐提升对御怨般若速度的要求。后者对拉条速度具有下限,但没有上限(只要低于御怨般若),且对御怨般若速度要求始终很高。注意按照不同的实际环境,选取不同的算法。
附录1:验证实验
验证实验1:
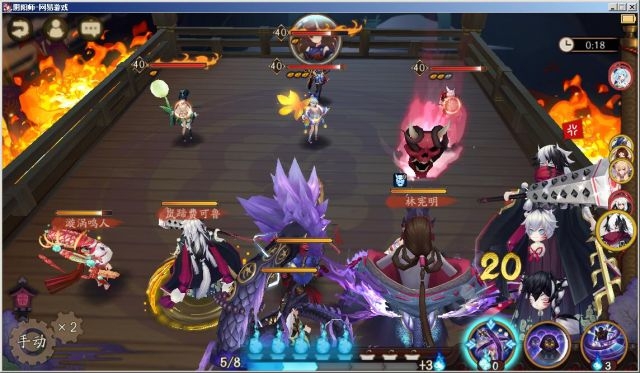
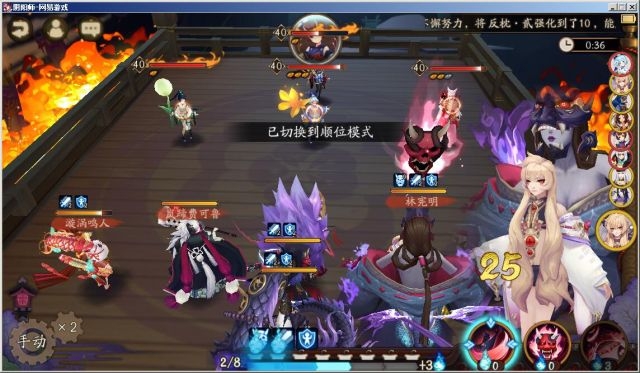
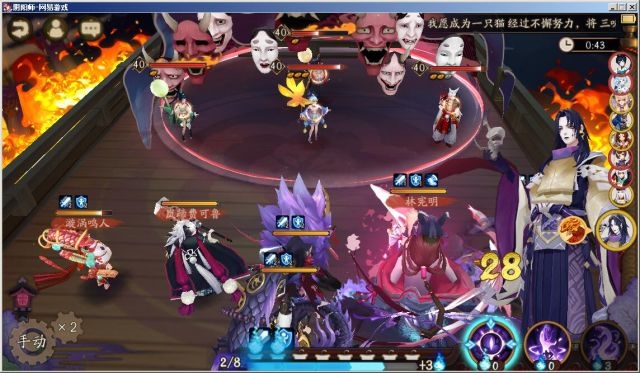
大蛇速度129,镰鼬速度182。
根据结论2-2-1,芋圆超车理论速度=129+182*0.65=247.3,芋圆实际速度248。
实验可见图中镰鼬行动时芋圆位置先于大蛇(第二轮御怨般若已跑距离大于等于低速已跑距离)。
实验可见图中镰鼬拉条后芋圆超车成功。
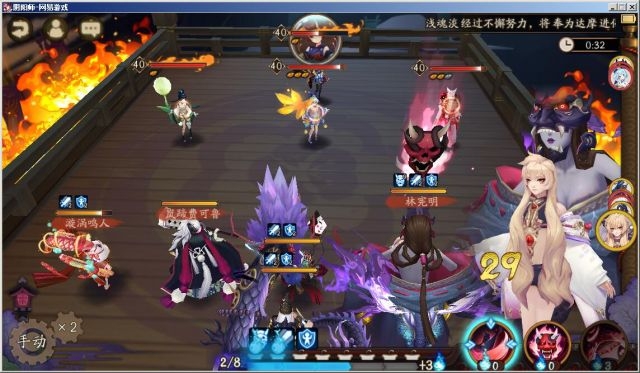
验证实验2:
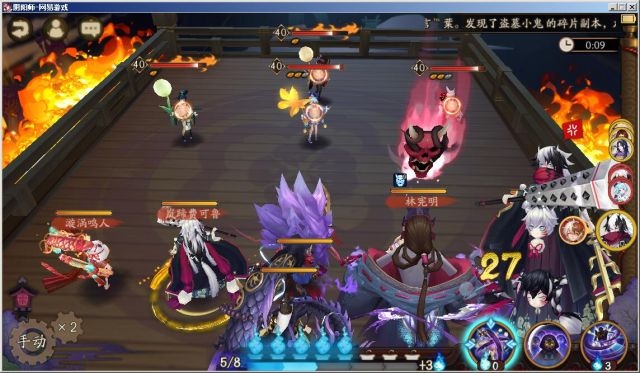
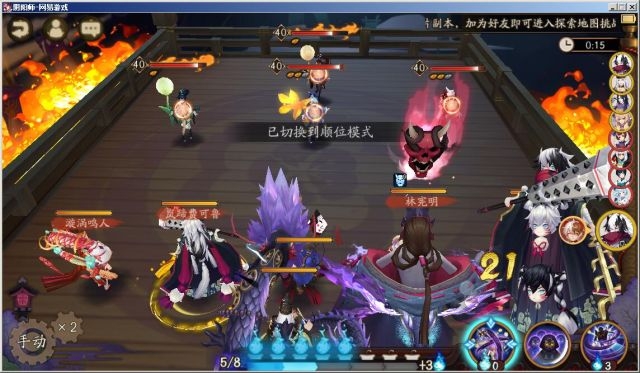
大蛇速度129,镰鼬速度227。
根据结论2-2-1,芋圆超车理论速度=129+227*0.65=276.55,该速度过高,难以轻易达到。
更换结论2-2-2,芋圆超车理论速度仅需高于250.71,芋圆实际速度251。
实验可见图中镰鼬行动时大蛇位置先于芋圆(第二轮御怨般若已跑距离小于低速已跑距离)。
实验可见图中镰鼬拉条后芋圆超车成功。
附录2:镰鼬山兔更换为蜜桃情形
更换为蜜桃后,拉条幅度由30%降低为25%。
注意:正式服神御已修改,不再对顺序靠前而位置不靠前的拉条,也不再对连续同一目标拉条。
对于结论2-2-1,拉条自身速度并无硬性上下限,御怨般若速度条件"需大于等于低速速度加上0.65倍的拉条速度"也与拉条幅度完全无关,因此结论2-2-1原封不动适用于蜜桃/神御。
对于结论2-2-2,拉条幅度对结论有影响。
重新计算原文三大前提可得(过程略):
(1)拉条速度需大于低速速度的4/3倍。
(2)芋圆速度需大于等于低速速度的28/15倍。
(3)芋圆速度需介于拉条速度的1倍到1.4倍之间。
综上所述,拉条更换为蜜桃后,
结论2-2-1完全不变:当阵容中有拉条时,若御怨般若快于拉条,若蜜桃行动时第二轮御怨般若已跑距离大于等于低速已跑距离,则御怨般若第二次行动超车己方低速必然成功。此时御怨般若速度需大于等于低速速度加上0.65倍的蜜桃速度。
结论2-2-2阈值改变:当阵容中有拉条时,若御怨般若快于拉条,若蜜桃行动时第二轮御怨般若已跑距离小于低速已跑距离,则御怨般若第二次行动若要超车己方低速,需要满足三个条件:拉条速度需大于低速速度的4/3倍、御怨般若速度需大于等于低速速度的28/15倍、御怨般若速度需介于蜜桃速度的1倍到1.4倍之间。
代入低速130,可得蜜桃版本的引申结论2-2-2
引申结论2-2-2:当阵容中有蜜桃时,若御怨般若快于蜜桃,设己方低速130,若蜜桃行动时第二轮御怨般若已跑距离小于低速已跑距离,则御怨般若第二次行动若要超车己方低速,蜜桃速度需大于173.33,御怨般若速度需大于等于242.67,且御怨般若速度需介于蜜桃速度的1倍到1.4倍之间。
ps.神御虽然和蜜桃同样拉条25%,但神御日曜界具有群体固定数值加速,视同"时机更晚的不知火先机加速",须考虑下文附录3情形,且神御拉条机制与其余任何拉条式神不同,因此神御不能照搬蜜桃结论。
ps.神御的算法较为复杂,改日尝试重新单独整理这一棘手的问题。
附录3:先机加速影响
无论哪一种超车情形,当具有先机加速时,芋圆和低速都将获得等值额外速度。然而超车理论要求芋圆速度远高于低速,因此等值额外速度对低速的提升比例一定高于对芋圆的提升比例,即低速跑条能力的增长幅度一定高于芋圆,因此必然导致芋圆超车难度加大。更有甚者,倘若拉条时,低速已跑完的距离已高于行动条的70%,则拉条将直接一拉到底,导致芋圆完全没有追赶余地,纵使芋圆速度突破天际也回天无力。
综上所述:一旦阵容包含先机加速,上文所有结论中的芋圆速度下限都将提升。务必在可选范围内进一步提高芋圆速度,否则将可能超车失败。
ps.先机群体加速目前通常指不知火的星火结界。稻荷神御馔津先机月影界加速仅作用于自身,视为仅影响变量"拉条速度"。稻荷神御馔津日曜界群体加速、追月神大招群体加速,代入本文时,近似视为"时机更晚的先机加速"考虑,亦同样导致芋圆速度下限提升,但影响幅度低于不知火。
ps.由于先机施展时机并非开场,而是敌我双方行动条首位式神到达行动条终点之时(如白藏主),故先机加速的作用时间并非从头到尾全程,亦因此导致具体计算极其复杂,故此处不再罗列公式,请自行根据上文结论中的速度下限进行适当提升后,穷举实测以寻找具体临界点。
ps.由于行动条首位式神只看先后,不看敌我,因此若敌方一速高于己方(包括白藏主),则先机加速的波动完全取决于敌方配速。此时预先估算精确下限已不可能办到。针对此情形,若非要在芋圆套圈阵容中使用不知火,则务必尽量提升芋圆速度,且尤其警惕敌方包含白藏主的阵容。